Как вычислить площадь трапеции: 6 простых способов

Трапеция – это четырёхугольник, у которого одна пара сторон параллельна, а другая нет. С 8 класса средней школы дети начинают проходить на уроках геометрии трапецию, её свойства, периметр и площадь. Очень часто задачи  на эту тему попадаются в заданиях ВПР (Всероссийских проверочных работ), ОГЭ, ЕГЭ, поэтому учителя сосредотачивают внимание детей на этой фигуре. В этой статье мы расскажем о том, что такое трапеция, о её свойствах и о 6 способах рассчитать её площадь.  

Что такое трапеция

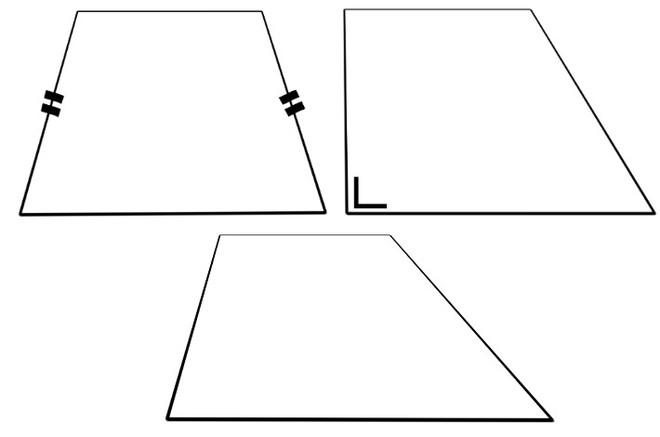
Для того чтобы рассчитывать площадь трапеции, нам необходимо узнать, что это такое, какие бывают виды, свойства этой фигуры и из чего состоит трапеция.

Для начала определение: трапеция – плоская четырёхугольная фигура, у которой две стороны параллельны, а другие две нет.

Виды трапеции

У каждого вида трапеции в зависимости от их свойств будут меняться формулы вычисления площади. Итак, трапеции бывают 3 видов.

1. Равнобедренные. Это такая трапеция, у которой длины непараллельных сторон равны, и углы их оснований тоже будут равны.
2. Прямоугольные. Это трапеция, у которой есть два прямых угла у оснований. Фактически ширина такой трапеции, перпендикулярная основаниям, является её высотой. 
3. Произвольные. Это такие трапеции, у которых все стороны разной длины, а углы произвольны.

Интересный факт: в 8 классе трапецию начинают изучать как подвид четырёхугольника, а вместе с ней параллелограмм и прямоугольник. И именно тогда мы узнаём, что параллелограмм и прямоугольник являются частными случаями трапеции.

Элементы трапеции

Рассказываем об элементах трапеции, с помощью которых мы будем рассчитывать площадь.

1. Основания трапеции. Это две противоположные стороны, параллельные друг другу.
2. Боковые стороны трапеции. Это те самые стороны, которые не параллельны и наклонены под углом. Если это равнобедренная трапеция, то наклонены они под одним углом и их длины равны, а если это прямоугольная трапеция, одна из сторон будет под углом 90 градусов.
3. Средняя линия. Это линия, соединяющая середины боковых сторон.

С помощью этих трёх понятий, а также диагоналей и углов трапеций, можно будет находить площадь.

Свойства трапеции

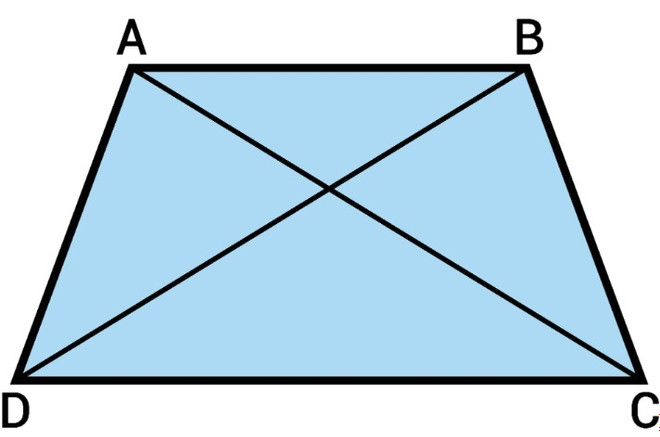
Поскольку трапеция – это четырёхугольник, то и некоторые свойства у неё будут схожи со свойствами квадрата, прямоугольника и параллелограмма. Однако у равнобедренной, произвольной и прямоугольной трапеции некоторые свойства будут отличаться. Мы расскажем обо всех.

Основные свойства произвольной трапеции:

1. Основания трапеции параллельны.
2. Средняя линия трапеции параллельна основаниям, считается она как полусумма этих самых оснований.
3. Сумма углов, прилегающих к боковой стороне, равна 180 градусам.
4. Средняя линия делит любой отрезок пополам, если его концы лежат на основаниях.
5. Точка пересечений диагоналей, середины оснований и точка продолжения боковых сторон лежат на одной прямой.
6. В трапецию, как и в любой другой четырёхугольник, можно вписать окружность, если сумма противоположных сторон будет равна.
7. Прямая, которая соединяет середины диагоналей, лежит на средней линии.

Основные свойства равнобедренной трапеции:

1. Углы при основаниях равны.
2. Такую трапецию можно описать окружностью.
3. Диагонали равнобедренной трапеции равны.
4. Так как углы при основаниях равны, то сумма углов составляет 180 градусов.

Основные свойства прямоугольной трапеции:

1. Высота прямоугольной трапеции – сторона, опущенная под 90 градусов к основанию.
2. В прямоугольной трапеции следующие углы: два прямых, один острый и один тупой.
3. Прямая, проведённая из вершины тупого угла и перпендикулярная основанию, делит трапецию на прямоугольник и прямоугольный треугольник.

Из этого множества свойств будут следовать почти все формулы нахождения площади трапеции, о которых мы расскажем далее.

Формулы вычисления площади трапеции

Теперь приступим к формулам нахождения площади трапеций. Их начинают изучать в 8 классе средней школы, а используют вплоть до 11 класса старшей школы. Эти формулы будут необходимы в стереометрии, когда надо будет найти площадь сложной трёхмерной фигуры. А задания на трапецию в ВПР, ОГЭ и ЕГЭ очень любят, могут их добавлять как в простые задачи из первых частей, так и в сложные во второй.

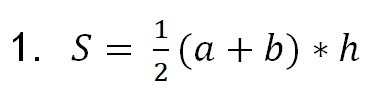
Это основная формула, к которой будут сводить другие. Здесь a и b – основания трапеции, h – высота трапеции.

Эта формула вытекает из понятия средней линии трапеции. Здесь MN – средняя линия, равная полусумме оснований

а h – высота трапеции.

Это способ, как найти площадь трапеции, если мы знаем значения длин её 4 сторон. Где a и b – основания трапеции, c и d – боковые стороны. В этой формуле первый множитель

 

можно заменить на обозначение средней линии – MN.

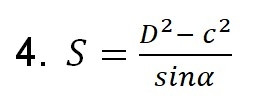
Этот способ нахождения площади подходит только для равнобедренной трапеции. Здесь D – диагональ трапеции, c – боковая сторона, α – угол у основания (sinα – отношение противолежащего катета к гипотенузе).

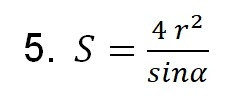
Эта формула также подходит только для равнобедренных трапеций, для  тех, в которых можно вписать окружность. Здесь r –  радиус вписанной окружности, α – угол у основания.

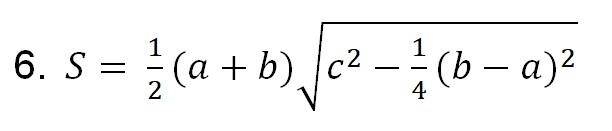
И эта формула также для равнобедренной трапеции. Здесь a и b – основания трапеции, с – боковая сторона.

Примеры задач

Для того чтобы лучше разобраться в материале, мы подготовили для вас задачи, которые будут решаться с помощью формул, которые мы представили выше. Мы расскажем алгоритм решения и покажем само решение.

Задача №1

Дана прямоугольная трапеция ABCD, основания BC и AD равны соответственно 5 см и 6 см, боковая сторона AB, перпендикулярная основанию,  равна 7 см. Найдите площадь трапеции.

Алгоритм:

Для начала мы должны записать в «дано», что нам известно из условия задачи. Затем необходимо записать, что нам требуется найти. Далее переходим уже к самому решению: рисуем заданную фигуру, отмечаем на ней длины известных сторон или градусные меры углов, затем пишем формулу, по которой будем искать площадь, после чего считаем значение. Записываем ответ, и задача решена.

Дано: ABCD – прямоугольная трапеция, BC = 5 см, AD = 6 см, AB = 7 см

Найти: S_ABCD – ?

Решение:

– по свойству прямоугольной трапеции

Ответ:  S_ABCD = 38,5 см² 

Следующие задачи решаем по такому же алгоритму.

Задача №2

В трапеции ABCD известна средняя линия, равная 15 см, и её высота, равная 5 см. Найдите площадь трапеции ABCD.

Дано: ABCD – трапеция, MN (средняя линия) = 15 см, CH (высота) = 5 см

Найти: S_ABCD – ? 

Решение:  S_ABCD = MN * h = MN * CH = 15 * 5 = 75 см²

Ответ: S_ABCD = 75 см² 

Задача № 3

В трапеции ABCD известны длины всех сторон: AB = 25 см, BC = 11 см, CD = 26 см, AD = 28 см. Найдите площадь трапеции ABCD.

Дано: ABCD – трапеция, AB = 25 см, BC = 11 см, CD = 26 см, AD = 28 см

Найти: S_ABCD – ? 

Решение:

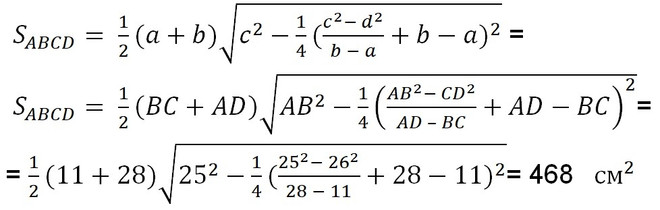
Ответ:  S_ABCD = 468 см² 

Задача № 4

Дана равнобедренная трапеция ABCD, в ней провели диагональ BD, равную 20 см, известна сторона AB – её длина составляет 12 см, угол <BAD равен 30 градусам. Найдите площадь равнобедренной трапеции ABCD.

Дано: ABCD – равнобедренная трапеция, BD = 20 см, AB = 12 см, <BAD = 30 градусов

Найти: S_ABCD – ?

Решение:

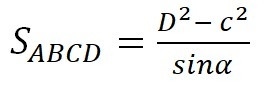
– по свойству диагонали в  равнобедренной трапеции

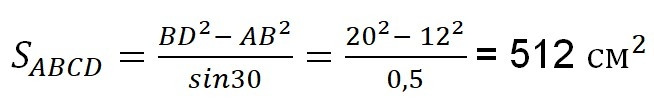
Ответ: S_ABCD = 512 см² 

Задача № 5

В равнобедренную трапецию ABCD вписали окружность радиусом 3 см. Угол у основания трапеции равен 60 градусам. Найдите площадь трапеции.

Дано: ABCD – равнобедренная трапеция, r = 3 см, α = 60 градусов

Найти: S_ABCD – ?

Решение:

– по свойству равнобедренной трапеции и вписанной в нее окружности

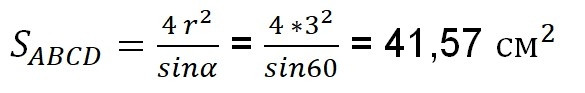
Ответ: S_ABCD= 41,57 см²

Задача № 6

Дана равнобедренная трапеция ABCD, известны её основания: AD = 10 см,  BC = 5 см, а также одна боковая сторона AB, равная 7 см. Найдите площадь трапеции.

Дано: ABCD – равнобедренная трапеция, AD = 10 см, BC = 5 см, AB = 7 см

Найти: S_ABCD – ?

Решение:

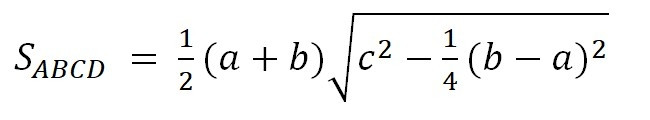
– по свойству равнобедренной трапеции.

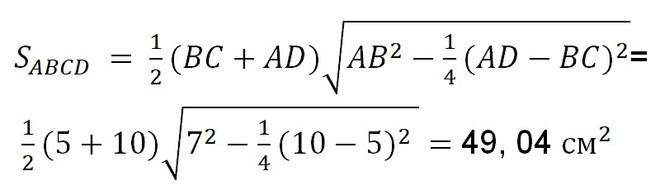
Ответ: S_ABCD= 49,04 см²