Периметр – это сумма длин всех сторон у любой плоской фигуры. Это одно из базовых понятий геометрии, которое начинают изучать во 2 классе начальной школы, а продолжают использовать вплоть до 11 класса. Нередки случаи включения задач на вычисление периметра в задания ВПР (Всероссийских проверочных работ), ОГЭ и ЕГЭ. В этой статье мы объясним, как считается периметр прямоугольника, дадим примеры задач и расскажем, как это может пригодиться в жизни.
Что такое прямоугольник

Прежде чем изучать периметр прямоугольника, надо для начала разобраться, что такое этот «прямоугольник».
Так вот, это четырёхугольник, у которого все углы равные и прямые, то есть по 90 градусов. Правильным прямоугольником является квадрат, а правильный он потому, что все стороны равны. У прямоугольника все стороны попарно параллельны, а это значит, что любой прямоугольник – параллелограмм.
Как понять, что выпуклый четырёхугольник является прямоугольником:
- Если у параллелограмма хотя бы один угол равен 90 градусов, то он прямоугольник.
- Если у параллелограмма равны диагонали, то этот параллелограмм является прямоугольником.
- Если параллелограмм диагонали делят на два равных и прямоугольных треугольника, то этот параллелограмм – прямоугольник
- Если у четырёхугольника 4 угла и все равны 90 градусов и стороны попарно равны и параллельны, то этот четырёхугольник – прямоугольник.
Свойства прямоугольника
Теперь нам необходимо разобраться со свойствами прямоугольника, так как из них мы потом получим различные формулы расчёта периметра или площади.
- Равенство противоположных сторон. Одно из важнейших свойств прямоугольника, которое напрямую влияет на вид формулы периметра фигуры.
- Каждый угол прямой. Это свойство исходит из определения прямоугольника.
- Равенство диагоналей. У прямоугольника равны диагонали, это прямые, соединяющие несмежные вершины геометрической фигуры
- Диагонали делят друг друга пополам. Это свойство распространяется на все прямоугольники, в том числе и на квадрат. Точка, в которой пересекутся две диагонали, поделит их пополам.
- Около любого прямоугольника можно описать окружность. Поскольку сумма противоположных углов в прямоугольнике даёт 180 градусов (так как каждый угол по 90 градусов), то вокруг него можно будет описать окружность с центром в точке пересечения диагоналей. Радиусом будет являться половина диагонали.
- Диагональ прямоугольника делит его на два прямоугольных треугольника. Это происходит из-за того, что в вершине получившегося треугольника будет угол, равный 90 градусам.
Каждое из этих свойств распространяется на все из существующих прямоугольников. Благодаря этим свойствам появляются различные формулы нахождения площади и периметра.
Формулы вычисления периметра прямоугольника
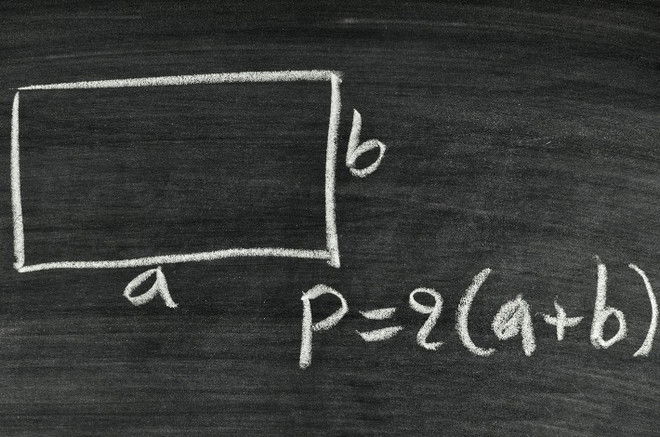
Вообще, периметр – это суммарная длина границ фигуры, если говорить простыми словами, то это сумма длин всех сторон геометрической фигуры. Общая формула вычисления периметра выглядит следующим образом:

Площадь и периметр являются базовыми понятиями геометрии, очень часто в начале обучения дети путают их друг с другом.
Разница между площадью и периметром заключается в следующем: периметр – длина внешних граней фигуры, измеряется она в метрах, сантиметрах, дециметрах и так далее, площадь же – это область пространства внутри любой фигуры, которая измеряется в квадратных метрах, квадратных сантиметрах и квадратных дециметрах.
Для каждой из фигур формулы вычисления периметра будут различные в зависимости от их свойств. В нашем случае у прямоугольника будут следующие формулы вычисления периметра:
1. P = 2 (a + b), где a – длина прямоугольника, а b – ширина.
Эта формула периметра исходит из свойства прямоугольника о равенстве противоположных сторон, поэтому изначальная формула с суммами длин всех сторон преобразуется в такую, где просто выносится общий множитель.
![]()
где a – сторона прямоугольника, а s – площадь прямоугольника.
Эта формула полезна, когда в задаче указана только одна сторона прямоугольника и его площадь. В данном случае мы фактически ищем сторону b через площадь, так как площадь прямоугольника – это произведение сторон.
![]()
где a – сторона прямоугольника, а d – диагональ прямоугольника
Эта формула используется в решении задач, где у прямоугольника известна диагональ и сторона. Фактически в этой задаче мы с помощью теоремы Пифагора ищем недостающую сторону b, а уже потом по классической формуле ищем периметр.
![]()
где a – сторона прямоугольника, а R – радиус описанной окружности вокруг прямоугольника.
В этой формуле – всё по той же теореме Пифагора: сначала с помощью радиуса описанной окружности находим диаметр прямоугольника, затем выражаем корень из разности диаметра и стороны и получаем вторую недостающую сторону. После чего по классической формуле ищем периметр.
С помощью этих формул вы можете решать задачи и самые лёгкие, и даже самые сложные. Также эти формулы помогут найти площади различных прямоугольников, а ещё они все применимы к квадрату – правильному четырёхугольнику.
Бывает такое, что фигура непростая – составная или сложная. Для того чтобы найти периметр составной фигуры, нам понадобится сложить длины его границ. Подобные задания очень часто встречаются не только в учебных материалах начальной школы, но и в вариантах ВПР и ОГЭ.
Примеры задач

Мы рассмотрим типы задач специально для каждой написанной нами выше формулы, чтобы вам было легче разобраться в данном материале.
Задача №1
Необходимо посчитать периметр прямоугольной площадки перед домом, чтобы понять, какое количество заборчика необходимо купить рабочим. Известно, что ширина площадки 3 метра, а длина – 7 метров.
Алгоритм:
Для начала, как и в любой другой задаче, мы должны записать, что нам дано и что требуется найти, затем, если нужно, перевести единицы измерения в систему СИ, затем приступаем к решению, а в конце уже пишем ответ.
Как это должно выглядеть в тетради:
Дано: a = 3 м; b = 7 м
Найти: P – ?
Решение: P = 2 (a + b)
– по свойству прямоугольника о равенстве противоположных сторон.
Pплощадки = 2 (3 + 7) = 20 м
Ответ: Pплощадки = 20 м – периметр площадки составляет 20 метров.
Последующие задачи необходимо решать по такому же алгоритму действий, чтобы не наделать лишних ошибок.
Задача №2
Для того чтобы положить плинтуса в комнате Вани, его папе нужно найти периметр комнаты. Он знает, что площадь комнаты составляет 20 квадратных метров, а длина одной стороны равна 5 метров.
Дано: S = 20 м2, a = 5 м
Найти: Pкомнаты – ?
Решение:
![]()
– по формуле нахождения площади прямоугольника и свойству равенства противоположных сторон
![]()
Ответ: Pкомнаты = 18 м – составляет периметр комнаты.
Задача №3
Необходимо посчитать периметр прямоугольника, известно, что его диагональ составляет 30 метров, а одна из сторон – 6 метров.
Дано: a = 6 м, d = 30 м
Найти: Pпрямоугольника – ?
Решение:
![]()
– по теореме Пифагора и свойству равенства противоположных сторон прямоугольника
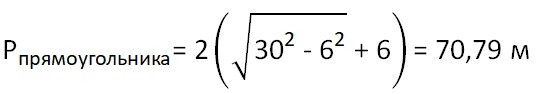
Ответ: Pпрямоугольника = 70,79 м
Задача №4
Вокруг старой прямоугольной клумбы сделали большую круглую песочницу радиусом 2 метра, известно, что одна из сторон бывшей клумбы составляла 50 см. Найдите периметр клумбы.
Дано: a = 50 см, R = 2 м
Найти: Pклумбы – ?
Решение:
![]()
– по свойству описанной вокруг прямоугольника окружности и равенства противоположных сторон.
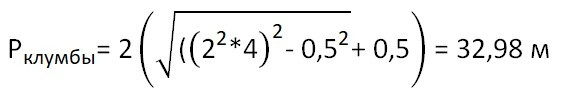
Ответ: Pклумбы = 32,98 м
Зачем нужно знать, как считается периметр
В принципе, геометрия – одна из тех наук, которые мы изучаем ещё с начальной школы и которая очень часто пригождается в реальной жизни.
Знание периметра поможет во многих областях, но особенно в строительном деле: нахождение длин ограждений и заборов, нахождение периметра и площади используется для заливки фундамента или для определения размера того или иного здания; в кулинарии: с помощью периметра находят размер пиццы, пирогов или размер форм для приготовления сдобных изделий; в картографии: здесь же периметр используют, очевидно, для нахождения расстояний от одного объекта до другого и, как следствие, для ориентирования на местности; в шитье, чтобы понять, какое количество ткани понадобится на одно или несколько изделий.
В общем, почти в каждой сфере деятельности – от архитектуры до кулинарии – используется понятие периметра.



