Квадрат – это правильный четырёхугольник, то есть плоская фигура с четырьмя равными углами, четырьмя равными сторонами. Его изучают со 2 класса начальной школы. Площадь квадрата можно вычислить разными способами, самый известный – сторона в квадрате. Об остальных расскажем в статье подробнее, а также приведём примеры задач разного уровня сложности.
Квадрат и его свойства

Квадрат – правильный четырёхугольник, у которого все 4 угла по 90 градусов и все стороны равны. Эту плоскую фигуру начинают изучать ещё с первых классов младшей школы и продолжают вплоть до 11 класса. И задачи с нахождением площади квадрата также усложняются по мере прохождения ребёнком школьной программы. Так, задачки начинаются с лёгкого варианта, где надо найти периметр, а заканчиваются вариантами по нахождению площади фигуры через вписанные и описанные окружности. Это мы ещё не говорим о том, что задачи на квадрат могут быть в вариантах ВПР, ОГЭ и ЕГЭ.
В стереометрии, геометрии в трёхмерном пространстве также любят внедрять в задачи квадрат и его свойства. Поэтому школьникам необходимо периодически решать задачи с квадратами, чтобы к концу 11 класса не забыть материал, который будет необходим для прохождения учебного материала и успешной сдачи экзаменов.
Давайте разберёмся со свойствами квадрата, которые используются повсеместно. Для этого нам понадобится начертить квадрат ABCD, провести две диагонали, пересекающиеся в точке O.
1. Начнём с того, что в принципе квадратом могут быть и параллелограмм, и ромб, и прямоугольник, если они соответственно имеют равные диагонали, углы и стороны.
2. Следующим свойством квадрата является равенство всех сторон.
AB = BC = CD = AD
3. Противоположные стороны квадрата параллельны друг другу, а смежные перпендикулярны.
AB || CD, BC || AD, AB ⊥ AD, AB ⊥ BC, CD ⊥ BC, CD ⊥ AD
4. Все четыре угла квадрата равны 90 градусов, в сумме – 360 градусов.
<ABC = <BCD = <CDA = <DAB = 90°;
<ABC + <BCD + <CDA + <DAB = 360°
5. Диагонали квадрата, так же, как и стороны, равны.
BD = AC
6. Диагональ квадрата разделят его на два и прямоугольных, и равнобедренных, и равных треугольника.
DAB = BCD; <BCD = <DAB = 90°
7. Диагонали квадрата пересекаются под прямым углом (то есть под 90 градусов, они перпендикулярны) и делят друг друга пополам.
AC ⊥ BD; AO = OC и BO = OD
8. В квадрат можно вписать окружность, так как сумма противоположных сторон будет равна. Это следует из второго свойства.
9. Квадрат можно описать окружностью, так как сумма противоположных углов составляет 180 градусов. Это следует из 4 свойства.
10. Из предыдущих трёх свойств следует, что точка пересечения диагоналей не только является центром квадрата, но также является центром вписанной и описанной окружностей.
11. Диагональ квадрата является биссектрисой прямого угла, то есть делит его пополам.
<BDA = <BDC = 45°;<ABD = <CBD = 45°
12. Если в квадрате провести две диагонали, то они создадут 4 равных равнобедренных и прямоугольных треугольника.
BOA = BOC = COD = AOD; BO = OD = AO = OC;
<COD = <COB = <AOB = <AOD = 90°.
13. Если мы соединим середины сторон квадрата, то получим квадрат в два раза меньше, так можно делать до бесконечности.
Вот какое большое количество свойств имеет казалось бы простая и эталонная фигура – квадрат! С помощью них выводятся теоремы и формулы вычисления площадей.
Формулы
Площадь квадрата – это величина, которая показывает, сколько места в пространстве занимает геометрическая фигура. Длина сторон может быть как и целым числом, так и дробями, и неизвестными. А измеряться эти числа могут не только в известных сантиметрах, но и в метрах, дециметрах, миллиметрах. Также для вычисления площади, возможно, понадобится решить уравнения с неизвестными.
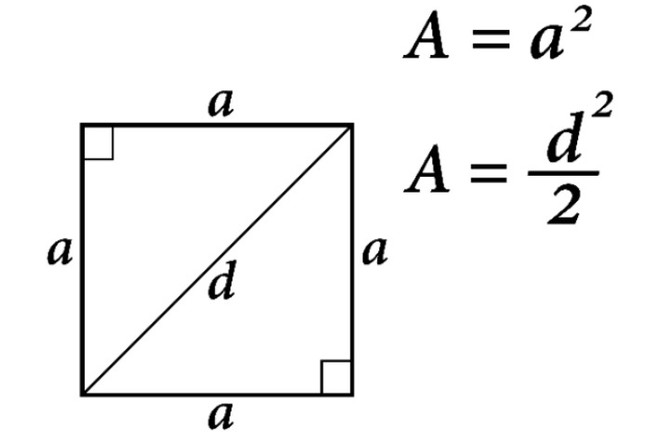
Теперь давайте перейдём к формулам площади.
Нахождение площади через длину стороны
Это самая известная формула площади квадрата, о которой рассказывают детям во втором классе начальной школы. Поскольку квадрат – это правильный прямоугольник, то есть прямоугольник, у которого все стороны равны, то мы можем воспользоваться формулой, суть которой в том, что для нахождения площади требуется всего лишь перемножить две стороны фигуры. А так как у квадрата все стороны равны, фактически мы перемножаем одну сторону на себя – мы можем взять одну сторону в квадрате и получим площадь квадрата. Вот так и получается самая известная формула вычисления площади квадрата:
S = a²
Нахождение площади через диагональ
Ещё одна не менее распространённая формула нахождения площади квадрата – через диагональ. Из теоремы Пифагора нам известно, что диагональ квадрата равна стороне, умноженной на корень из 2.
Так вот, чтобы привести формулу к изначальному виду, нам необходимо длину диагонали возвести в квадрат и поделить на 2, чтобы таким образом избавиться от двойки. Так мы получаем ещё одну формулу площади квадрата через диагональ.
![]()
Нахождение площади через радиус вписанной окружности
Мы уже говорили о том, что в любой квадрат мы можем вписать окружность. Это означает, что с помощью вписанной окружности мы также можем найти площадь квадрата. Радиусом вписанной окружности будет являться половина стороны квадрата, и, чтобы с помощью него найти площадь, нужно снова приводить формулу к изначальному виду. Для этого нам необходимо возвести радиус в квадрат и умножить его на 4. Таким образом, мы вывели ещё одну формулу нахождения площади квадрата с помощью радиуса вписанной окружности.
S = 4 * r²
Нахождение площади через радиус описанной окружности
Вокруг квадрата возможно описать окружность, в таком случае радиусом этого самого круга будет являться половина диагонали квадрата. Как нам известно, по теореме Пифагора, диагональ будет равна стороне, умноженной на корень из двух, а половина диагонали будет являться стороной, умноженной на корень из двух и ещё делённой на два. Снова по той же схеме приводим формулу к изначальному виду и получаем новую формулу нахождения площади квадрата через радиус описанной окружности.
S = 2 * R²
Нахождение площади через периметр
Для начала стоит сказать, что периметр – это сумма длин всех сторон. Поскольку у квадрата все стороны равны, то периметр будет равен стороне, умноженной на 4. Из этого мы можем вывести ещё одну формулу площади квадрата, выразив сторону. В итоге мы получаем:
![]()
С помощью всех этих формул дети, начиная со 2 класса начальной школы и вплоть до 11 класса старшей школы, вычисляют площадь квадрата в задачах различной сложности.
Примеры задач

Для того чтобы вам было проще понять, как считать площадь квадрата, мы подготовили несколько задач разной степени сложности. В каждой из них основная цель – вычислить площадь квадрата, однако сделать это надо будет разными способами.
Задача №1
Дана сторона квадрата, равная 5 сантиметрам. Вычислите площадь фигуры.
Алгоритм:
Как всегда, чтобы начать решать задачу, необходимо выписать, что нам известно в «дано». В нашем случае нам известно, что сторона квадрата равна 5 сантиметрам. Далее необходимо указать, что нам надо найти. Затем нарисуйте квадрат для визуального удобства, а потом уже приступайте к решению.
Как это должно выглядеть в тетради:
Дано: a = 5 см (очень важно обратить внимание на то, что у всех единиц СИ мы не ставим точку для сокращения, это будет считаться ошибкой)
Найти: SABCD - ?
Решение: SABCD = a² = 5² = 25 см – по свойству квадрата и прямоугольника
Ответ: SABCD = 25 м²
Вот и вся задача! Последующие задачи рекомендуем выполнять по такому же алгоритму.
Задача №2
Мама Вани хочет купить ковёр к нему в комнату, но не знает, какой размер стоит выбрать. Ваня решил помочь маме купить ковёр и измерил диагональное расстояние от кровати до тумбочки у кровати, оно равно 1,5 метрам. Какого размера стоит купить ковёр?
Дано: d = 1,5 м
Найти: Sковра - ?
Решение:
![]()
– по свойству диагонали квадрата
Ответ: Sковра = 1,125 м²
В подобных задачах могут попросить перевести метры в сантиметры, внимательнее читайте условие.
Задача №3
На дачном участке хозяева решили поставить колодец радиусом 50 сантиметров. Какой площади квадрат должны вырыть рабочие, чтобы поместилась труба от колодца?
Дано: r = 50 см
Найти: Sквадрата - ?
Решение: Sквадрата = 4 * r² = 4 * 50² =10 000 см² – по свойству вписанной окружности в квадрат.
Ответ: Sквадрата = 10 000 см²
Задача №4
Вокруг старой песочницы жители многоквартирного дома решили сделать клумбу. Какая была площадь старой песочницы, если у получившейся клумбы радиус составил 1,5 метра?
Дано: R = 1,5 м
Найти: Sпесочницы - ?
Решение: Sпесочницы = 2 * R² = 2 * 1,5² = 4,5 м² – по свойству описанной окружности вокруг квадрата.
Ответ: Sпесочницы = 4,5 м²
Задача №5
Бабушка хочет оградить свою грядку площадью 3 квадратных метра. Какой длины заборчик ей понадобится?
Дано: Sгрядки = 3 м²
Найти: p – ?
Решение:
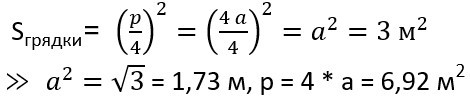
– по свойству периметра квадрата.
Ответ: p = 6,92 м



